Inverted-U graphs and Testing
towards an optima for test effectiveness + why getting there is hard
I.
I like simple graphs.
Because I think the best graphs are the ones that get the point across quickly. Exponentials (number go up) and logarithmic curves (diminishing returns) being the quintessential examples. Simple, shareable and ideally slightly sensational. Anything more complicated than that and it usually needs an accompanying blog post.
P.S: If you want to lie to a large audience, the best way to do it is probably with graphs. Painfully few people are on the lookout for graph crimes.
lies, damned lies, and badly scaled graphs - every internet user
But just because they can be wielded poorly, doesn't mean they aren't a versatile way to explain phenomenon. Take for example, the humble inverted-U graph.
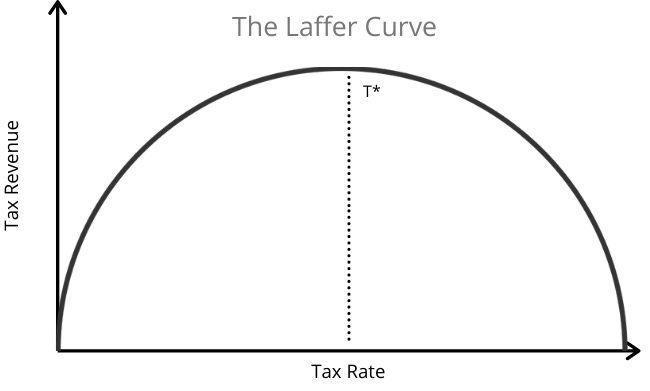
It shows up in a lot of places. For example, an economic theory called the Laffer curve, which tries to show the existence of an optimal tax rate.
The basic idea is that if you tax your citizens too much, some of them may stop working. Others may leave the country or decide that committing tax fraud is cheaper than paying up. So you end up with lower tax revenue overall.
Obviously, if you tax too little, you're gonna end up with less than optimal tax revenue by definition. There's a sweet spot that is "just right". And the challenge is finding it.
There's also the Yerkes-Dodson law which graphs the relationship between stress and performance. Too little stress, and the performer isn't actively engaged. Too much, and their composure breaks.
The point being, most things have a relationship like the above phenomenon. There's an ideal degree of use, past which you get lower returns. And with too little, you miss out on maximimal benefit.
II.
And this is how most tests work too.
Look at the field of physical performance, for example. Where they have a bunch of really simple tests. There's sprint tests over varying distances, medicine ball tosses, squat maxes, vertical jump tests, etc. Any basic movement you can think of can be used as a test.
That’s because it’s costly to assess the sport directly. Both in terms of replicating the competitive environment as well as fatigue. We need ways to measure often and it’s infeasible to do that if your test is expensive. Like it usually is due to the complexity and detail inherent to specific tests.
Furthermore, most events involve a bunch of co-ordinated sub-routines where isolating a clear data point is difficult, to say the least.
If a long jumper wants to test lower limb explosive strength, they're better off measuring their standing vertical vs. an entire long jump trial (which involves an accurate run-up, take-off and landing sequence, each made up of even smaller parts). A larger surface area allows more noise to creep in.
So what if you wanted to pick the athletes with the best potential for high-power events like the sprints and jumps? You choose a simple test, say, standing broad jump. You put people through it, and it seems to give you clear, unbiased results. And you pick the ones who are obviously incredible at the simple movements being tested. They’re the best, right?
Well, not quite.
In the case of the broad jump test, factors like optimal shin angles, arm swing and landing mechanics play a fairly big role in determining the final distance jumped. Somebody who's practiced this before, even if it's just for fun, would have a pretty significant advantage. Even simple tests have technique-based advantages.
This isn't actually a problem though, you do want to select for people who are athletic enough to have jumped before in their lives. In general too, you don't really want to test for purely inate talent. It's important to select people who have previous experience with specific-but-not-too-specific tests, it’s often a signal of an independent interest in the field. Jumping for fun is to athletics what the ability to touchtype is to programmers.
Something like a isometric mid-thigh pull is an easy test to administer, but it tells you virtually nothing about specific strengths. A world class sprinter and a 300lb powerlifter would give you similar numbers. Too general is as bad as too specific when it comes to providing useful data.
III.
What about the degree of difficulty?
Obviously, a test that's too easy doesn't help much (on it's own). But what it does do is shore up the bottom. Even a small filter gets you pretty efficient benefits. Just like how going from free to a penny can cause a huge drop in demand, a non-zero difficulty in entry usually gets rid of the most undesirable candidates.
Something like the SAT, where perfect scores are common, doesn’t work as a signal for genius. But at least it filters out the slackers. Which is all a test should aim for, in my opinion.
Too difficult, and you start to select for test-takers. Folks who are willing to spend time optimising for your examinations. This works pretty well if you're an employer who needs nothing more than people willing to work 100 hour weeks. If they're going to work with/for you, at least you’re sure they’re the folks willing to put in the work.
But this only selects for a specific type of raw work ethic1. If you want to find people who are doing cooler things than test-prep, you shouldn’t go searching with a really tough test as your only filter.
The other problem with too-difficult assesments is that at the extreme right tail of the distribution, the differences between candidates is often pure luck. Which can lead a significantly less-than-ideal outcomes for the test takers.
IV.
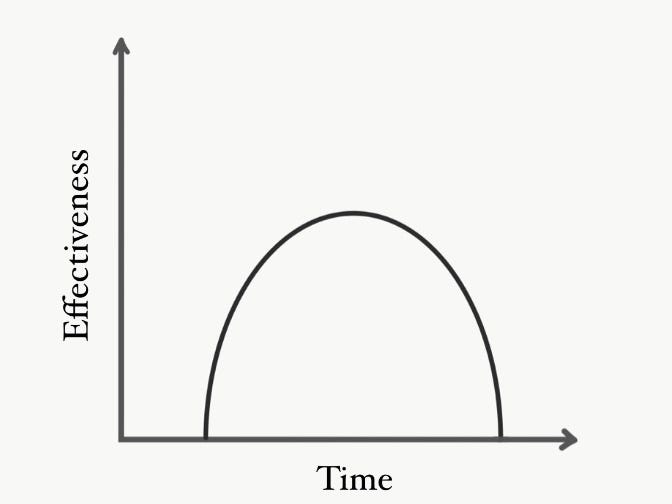
Finally, allow me to present the Time-Effectiveness graph.
Usually, a completely new test works very well for finding raw talent. The true, hardcore enthusiasts will be most ready for it. The downside is you'll only select the ones that are the very best at that particular moment. Leaving out the merely-good-but-with-potential folks that you need to fill the ranks.
Some tests require a period of acclimatisation, during which they’re stuck in the Point of Unavoidable Noise. It might take months before an athlete's power clean technique allows them to express their true limb strength. During that learning period, any data gathered from the movement will be extremely noisy.
But if a test's been around too long, it gets gamed. This seems to be an inexorable law, as far as I can tell. Really difficult tests gatekeep the most desirable outcomes. Outcomes, in turn, are judged desirable by their historic ROI.
So as a general rule, the older the test => the harder the test => the more the benefit of gaming it will be.
Most people do not want to lie on their college admission essays. At least, I hope they don’t. But college is a big deal, and essays have been around long enough for them to learn what they admissions office is looking for. I don’t blame students for giving them what they want to hear.
The optimal point is therefore the place where most people have enough experience with the test that they stop seeing large improvements from test/technique specific inprovements. And talent has a chance to come through again.
V.
The solution? I don't have one.
As far as I can tell, large scale effective testing is a human compete problem as well as an adverserial system. A messy domain, where being complacent about the methods you use just doesn't cut it.
Which is why organisations have evolved a bunch of different testing mechanisms, ranging from the standardised multiple-choice test to multiple rounds of personal interviews. And even these have started to fail with time.
Workarounds like referalls only work on a small scale. Letting people who've already done the testing tell you how good a candidate is useful, no doubt. But they're subjective and domain specific, making them hard to scale up or generalize. So the problem still exists in the newbie phase (which is where most testing happens anyway) and for people who want to hop across domains.
That being said, here's a few suggestions:
You can try switching up your tests often to make them harder to game, but that's expensive. And there's still the initial Point of Unavoidable Noise that comes with introducing a new method of testing.
You could use multiple tests hoping for more predictice power, but that's also inefficient and costly. Plus people who game a particular test are usually good at gaming tests in general. So you might just end up selecting for the ultimate test-taker.
Another method involves letting candidates provide their own alternatives to testing, usually involving some sort of proof of work. While this does mean that it's harder to gauge weaknesses, knowing what they consider thier strengths is valuable information. Not every domain is suited to this......
If you've got relatively little to lose, you can afford to operate with close to no testing. You can choose to trust random chance, using lotteries to make your choices. (I'm serious, there is often significant alpha to be found in random bets.)
Lotteries are especially effective if you're picking from the top percentiles of a group2. Where success is determined relatively heavily by test-taking ability vs. actual ability. In that case, what you're looking for isn't really the 99th percentile (people optimised for test-taking), but more around the 95th (decidedly smart, but optimising for more relevant stuff).
Like any tool that relies on dimension reduction, the problems with testing are the loss of detail. The price for legibility and efficiency is variance. It seems like the meta solution here is to ensure that there are viable alternatives to traditional testing processes. This should shift incentives away from already overcrowded funnels, and encourage competition along multiple axes. More playgrounds = more fun for everyone involved.
Honestly, it would be really convenient if that’s all it took to solve problems in the messy real world. Just round up a bunch of hard-working folk and let them usher in utopia.
Elite universities are the funny places where lotteries would probably bring the most…ahem, interesting outcomes, but would be the last to adopt them.